2014国家公务员考试行测数量关系练习4
1.某年级组织一次春游,租船游湖,若每条船乘10人,则还有2人无座位;若每条船乘12人,则可少用一船,且人员刚好坐满,这时每人可节省5角钱。问租一条船需要多少钱?( )
 相关文章
相关文章
A. 9元
B. 24元
C. 30元
D. 36元
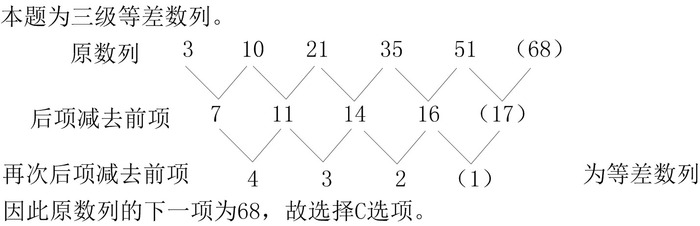
2.3,10,21,35,51,( )
A. 59
B. 66
C. 68
D. 72
3.骑自行车从甲地到乙地,以10千米/时的速度行进,下午1时到;以15千米/时的速度行进,上午11时到。如果希望中午12时到,那么应以怎样的速度行进?( )
A. 11千米/时
B. 12千米/时
C. 12.5千米/时
D. 13.5千米/时
4.22,24,39,28,( ),16
A. 14
B. 11
C. 30
D. 15
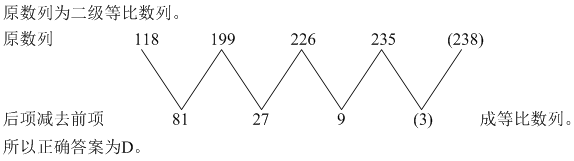
5.118,199,226,235,( )
A. 255
B. 253
C. 246
D. 238
6.一个三位数除以43,商是a,余数是b,则a+b的最大值是( )。
A. 957
B. 64
C. 56
D. 33
7.一批商品,按期望获得50%的利润来定价,结果只销售掉70%的商品,为尽早销售掉剩下的商品,商店决定按定价打折出售,这样所获得的全部利润,是原来所期望利润的82% ,问打了多少折扣?( )
A. 4折
B. 6折
C. 7折
D. 8折
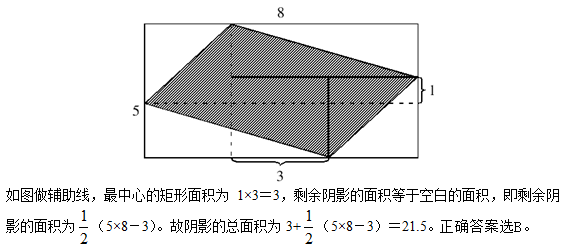
8.长为8宽为5的长方形内有一内接阴影四边形(如图所示),则阴影四边形的面积是( )。
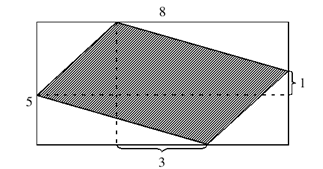

A. 15.5
B. 21.5
C. 20.5
D. 20
9.甲、乙两人沿直线从A地步行至B地,丙从B地步行至A地。已知甲、乙、丙三人同时出发,甲和丙相遇后5分钟,乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问A、B两地距离为多少米?
A. 8000米
B. 8500米
C. 10000米
D. 10500米
10.从一楼走到五楼,爬完一层休息30秒,一共要210秒,那么从一楼走到7楼,需要多少秒?
A. 318
B. 294
C. 330
D. 360
11.5,24,6,20,( ),15,10,( )
A. 7,15
B. 8,12
C. 9,12
D. 10,10
12.将104张桌子分别放到14个办公室,每个人办公室至少放一张桌子,不管怎样分至少有几个办公室的桌子数是一样多?( )
A. 2
B. 3
C. 7
D. 无法确定
13.某年10月份有四个星期四,五个星期三,这年的10月8日是星期( )。
A. 一
B. 二
C. 三
D. 四
14.2,3,7,16,65,321,( )
A. 4542
B. 4544
C. 4546
D. 4548
15.某公共汽车从起点站开往终点站,途中共有13个停车站。如果这辆公共汽车从起点站开出,除终点站外,每一站上车的乘客中,正好在以后的每一站有一位乘客下车。为了使每位乘客都有座位,那么,这辆公共汽车至少应有多少个座位?( )
A. 48
B. 52
C. 56
D. 54
江苏启禾教育答案解析:
江苏启禾教育答案解析:
1.设船数为X,由题意得10X+2=12(X-1),解得X=7,所以人数为10×7+2=72人。每个人省5角钱,则72个人共省5×72=360角=36元,即租一条船需要36元,故正确答案为D。
2.

3.设总路长为S,则有S÷10-S÷15=2,解得S=60,所以出发时间是上午7点,要想中午12点到,则速度应为60÷5=12千米/时。故正确答案为B。
4.原数列22、24、39、28、( )、16中各项十位上的数除以个位上的数的值分别为2÷2=1,4÷2=2,9÷3=3,8÷2=4,是一个等差数列(6÷1=6满足此分析),因此下一项十位上的数除以个位上的数应该为5,选项中只有D符合。故正确答案为D。
5.

6.假设被除数为M,则可得M=43a+b。由余数≥0,可知43a≤M≤999,解得a≤23。若a=23,而M最大为999,此时得到余数最大为10,两者之和为33;若a=22,由余数小于除数,即b<43,可知b≤42,只需看b=42是否能够取到,此时反向构造被除数=43×22+42=988,仍为三位数,满足要求。此时a与b之和为64。注意题目中的A选项显然不可能,在剩余三个选项中,64已经是最大值,无需继续尝试。故正确答案为B。
7.设共有商品10件,每件成本为10元,则原定价为10×(1+50%)=15元,共卖出10×70%=7件商品,利润为10×50%×7=35元,剩余3件。10件商品总利润为10×10×50%×82%=41元,设剩余3件所打折扣为x,则由题意得35+(15x-10)×3=41,解得x=0.8,故正确答案为D。
8.

9.本题理解的重点在于:在甲和丙相遇时,甲比乙多走的距离为后来乙丙一起走的距离。有了这个思想,就容易解出,甲和丙相遇时,甲比乙多走的距离为(75+65)×5=700m,假设甲和丙相遇的时候,甲走了a分钟,则(85-75)a=700,解得a=70。所以两地相距为(85+65)×70=10500米,故正确答案为D。
10.从一楼走到五楼,休息了3次,那么每爬上一层需要的时间为(210-30×3)÷4=30秒,故从一楼走到七楼需要30×(7-2)+30×(7-1)=330秒。故正确答案为C。
11.两两分组:[5,24] [ 6,20] [ ( ),15] [ 10,( )]
组内做积: 120 120 120 120
各组所得积值构成常数数列,故未知项分别为8、12。
所以正确答案为B。
12.若要让办公室中桌子数不同,可以每个办公室桌子数分别为1、2、3、4、…、13、14张,那么14个房间需要(1+14)×14÷2=105张,因此只能有一个办公室中桌子数减少105-104=1张,所以最少有2个办公室的桌子数是一样的。故正确答案为A。
13.10月共31天,有五个星期三,则第五个星期三可能是29、30、31号,星期四只有四个,则第五个星期三只能是31号,因此10月1号为星期一,10月8号为星期一,故正确答案为A。
14.

15.根据题目可知起点站上14人,第一停车站上13人,下1人;第二车站上12人,下2人;第三停车站上11人,下3人;……;第十三停车站上1人,下13人。分析可知,上车人数随站递减,下车人数随站递增,所以当下车人数等于上车人数时,车上人数最多,第七停车站上7人下7人,所以此时人数达到最多,以后递减,此时人数为14+(13-1)+(12-2)+(11-3)+(10-4)+(9-5)+(8-6)=56,因此这辆公共汽车至少应有56个座位,故正确答案为C。
 相关文章
相关文章